GHHF vs Self-Leverage

-

GHHF has now been available for over a year, providing us with an opportunity to compare its real-world performance against a hypothetical self-leveraged portfolio. While both aim to boost returns through debt, there are critical differences in rebalancing, currency exposure, fees, and tax implications that can sway the outcome.

The motivation is GHHF has access to cheaper debt than most can get via there mortgage, so is it worth moving over to it? Or do the other costs decay its lead?

The idea is to compare GHHF to self-leverage, that is buying the same assets with the same amount of debt where the debt is obtained via debt recycling or an equity release.

Disclaimer: I'm no expert at doing these comparisons, so take everything with a grain of salt.

TLDR

GHHF and self-leverage have delivered remarkably comparable returns over the past year of 17.6% pa vs 17.7% pa.

Differences

While I attempted to keep the differences to a minimum, there are a few differences between the two options, making it not exactly a like for like comparison.

Rebalancing

A key differences is self-leveraged will not rebalance. Perhaps later I'll rebalance yearly.

Rebalancing has both positive and negative impacts, so it will be interesting to see which way the last year goes. In a sideways market rebalancing can negatively impact GHHF, while in an rising market it can benefit GHHF.

Currency Hedging

I believe GHHF has additional currency hedging beyond using HGBL. I have not accounted for this.

Interest and Fees

GHHF fees are 0.35%. It is speculated that the internal interest rate is the cash rate + 1%, so about = 4.25% + 1% = 5.25% over this period

So I expect the total cost to be around 5.60%.

Meanwhile, P&I mortgages over the same period are around 6.16%, thus GHHF has an edge for its cheaper debt.

GHHF is effectively interest only, while self-leveraged will be Principal and Interest in this comparison. 

Method

  1. Use waybackmachine.com to find the earliest possible gearing ratio and allocations.
  2. Purchase $100,000 of GHHF on Sharesight
  3. Purchase the equivalent underlying assets in Sharesight using the same amount of debt from the mortgage.
  4. Compare the difference in return against the amount borrowed

Research



Not ideal that the asset allocation date is a bit earlier, however the key part is the gearing ratio so I'll go with that date for the purchase.
  • 22/MAY/2024
    • Gearing Ratio: 33.9%
  • 30/APR/2024
    • Australian Equities: 35.0%
    • US Equities: 42.4%
    • Developed Markets - Ex US 16.0%
    • Emerging Markets: 6.6%
And the allocations are:
  • A200: 35.0%
  • BGBL: 37.4%
  • HGBL: 21.0%
  • IEMG: 6.6%
Notes: IEMG is in USD so a bit trickier than the rest to determine. On the purchase date it was trading at 54.25 USD, and we need to purchase $9,985 AUD at AU$1 = US$0.66186876, so we will buy 122 units.

The split between HGBL and BGBL is not explicitly stated on the GHHF page, so I am using PIA allocation of 44% to BGBL + IEMG, and the remainder of 21.0% to HGBL.

The amount of debt used on the 22/MAY/2024 for $100,000 of GHHF is:

Debt = $100,000 / (100% - 33.9%) - $100K = $51,285

Assets = $100K + $51,285 = $151,285

Sharesight

Purchases on 22/MAY/2024
  1. GHHF 3796 units @ $26.35 = $99,998.25
  2. A200 403 units @ 131.41 = $52,958.23
  3. BGBL 888 units @ $63.73 = 56,592.24
  4. HGBL 507 units @ $62.63 = $31,753.41
  5. IEMB 122 units @ $54.24 USD = $9,999.72 AUD

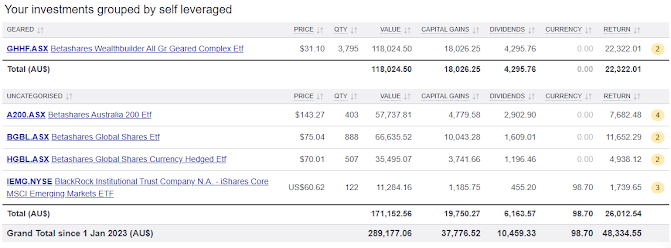
Results

As of the 5/JUL/2025, we get these results in Sharesight.


Duration = (5/JUL/2025 - 22/MAY/2024) / 365 =  1.12 years.

Mortgage Cost = 6.16% pa

The overall returns are
  • Self-leverage: $22,472 or 17.7%
    • Market = $26,102 (excluding debt cost)
    • Debt = $51,285 x 6.16% x 1.12 years = $3,540
    • Total = Return - Debt = $26,012 - $3,540 = $22,472
    • Return % = (1 + 22,472 / 100,000 / 1.12 years) ^ (1 / 1.12) - 1 = 17.7%
  • GHHF: $22,322 or 17.6%
    • Market = 22,322
    • Return % = (1 + 22,322 / 1.12) ^ (1 / 1.12) - 1 = 17.6%
Overall, a very similar return with self-leveraged getting slightly ahead.

So in order to match the return of GHHF, we need to pay an interest rate of:

GHHF Comparison Rate = (26,012 - 22,322) / 51,285 / 1.12 years = 6.42%

Annualising Interest Rates

I sat far too long pondering if I annualise the interest rates with or without compounding.

In the end I went without compounding, with the justification being that inside GHHF the interest is paid by reducing the return, and its the after costs return that compounds.

In addition I did not turn on dividend re-investment on share sight, so the self-leveraged will have enough dividends to cover the interest bill.

Tax Deductibility

The interest rates above are all pre-tax. 

Something that is not immediately obvious is if the internal GHHF tax is tax deductible. And the answer is that it effectively is. This happens because the interest expense is implicitly deducted before the final income distribution is calculated and passed onto you. So, while you don't claim the interest expense separately on your tax return like with self-leverage, the net taxable income you receive from GHHF has already factored in this deduction.

You can also see this in the following formula.

MTR = Marginal Tax Rate

After Tax Return = Dividend x (1 - MTR) - Interest x (1 - MTR) = (Dividend - Interest) x (1 - MTR)

That is, you can think of the tax in 2 ways
  1. Claim the dividends and interest separately
  2. Claim the dividends minus interest 
Thus tax wise GHHF and self-leverage are the same.

This means if your marginal tax rate decreases significantly in retirement, the effective tax benefit of GHHF's internal leverage also diminishes, making the overall cost of that leverage higher on an after-tax basis. 

In order to deleverage GHHF you need to sell, and protentional pay a higher amount of capital gains tax.

In contrast, with self-leverage, you retain control over the loan and its repayment without having to sell. 

Conclusion

Overall the difference in the expected returns are comparable. As such, the return is not the primary reason to choose one over the other.

Data


Checking the RBA Dataset F5 "Lending rates; Housing loans; Banks; 3-year fixed; Owner-occupier" (I find this the closest match to current competitive variable rate), the home mortgage rate over that period is around 6.16%.

Further Reading

Comments

Post a Comment

Popular posts from this blog

DIV 293 Tax

-
I'm considering the impact of DIV 293 on my possible IP sale, so lets see what its all about. DIV 293 tax is a fun one as it works on the lessor of two amounts. Thus some funky things occur. Now lets put aside the very good point that focusing on reducing tax is a terrible strategy, and focus on reducing tax. Formula If  DIV 293 Income > $250K  then DIV 293 applies. If  Super < Income + Super - $250K  then  Super Assessed  Else  Income + Super Assessed Note:  Income  on this page means all DIV 293 Income excluding Super. Hold My Triple Venti Half-Caf Soy Latte Wait a second, I see something... = Super > DIV293 Income + Super - $250K = Super - Super > DIV293 Income + Super - $250K - Super  (Subtract Super both sides) = 0 > Income - $250K  (Eliminate) = Income - $250K < 0  (Reverse) = Income - $250K + $250K < 0 + $250K  (Add $250K both sides) = Income < $250K Oh, I did not expect to simplify what it t...
Read more

Finance Battle: HISA vs FHSSS

-
Image
In this lineup let's see the difference in FHSSS and HISA. FHSSS $10K put into FHSS ends up as $8,500. Lets assume 4% deeming rate, so you can withdraw =$8,500 x 104% = $8,840. Now you withdraw with MTR 32%: = 8,840 x (100% - 32% + 30%) = $8,663.2 MTR 39%: = 8,840 x (100% - 39% + 30%) = $8,044.4 MTR 47%: = 8,840 x (100% - 47% + 30%) = $7,337.2 HISA $10K income into HISA. Lets assume 5.5% return. MTR 32%: = 10,000 x (100 - 32%) x (100% + 5.5% x (100% - 32%)) = $7,054 MTR 39%: = 10,000 x (100 - 39%) x (100% + 5.5% x (100% - 39%)) = $6,304 MTR 47%: = 10,000 x (100 - 47%) x (100% + 5.5% x (100% - 47%)) = $5,454 FHSS Relative Improvement Relative to HISA So how much better if FHSS after just 1 year? MTR 32%: = (8,663.2 - 7054) / 7054 = 22.8% MTR 39%: = (8,044.4 - 6304) / 6304 = 27.6% MTR 47%: = (7,337.2 - 5454) / 5454 = 34.5% ANZ FHSS Calculator This calculator compares over 4-7 years which is an improvement over my above calculation. I believe it also includes the impact of the withdr...
Read more

Debt Recycling and the Offset Fallacy

-
Image
A common miss-conception that caught me out for longer than I want to admit is the difference in 'making money' and 'no longer spending money'. When you use your offset you are 'no longer spending money', however I mistakenly thought of it as 'making money'. This meant I often miss-calculated investing while I have a mortgage. Credit Card Think of your credit card. If you spend $1,000 you start paying interest. If you repay the $1,000 you stop paying interest. Now the question, are you saving 20% pa x $1,000 forever by paying off the credit card? How do we account for the interest we no longer pay because we paid the credit card off?  I ignore it, and this applies to my offset too. The Offset Fallacy The example that made me see offsets differently was to imagine my current situation, lets say I've got a $200K mortgage with $100K in the offset. Now imagine you are debt free, and go and borrow $200K, park $100K in the offset and spend $100K on a nice ...
Read more